Test report・Estimating latent bugs by reliability growth curve

14/07/202121/10/2021Test qualityy

Write an estimated number of bugs not found in the software test report

Write the test result and test evaluation in the test report of the software . Simply put, the status of the bug detected in the test is the test result, and the quality of the test work is the test evaluation. I write the status of the bug in this test result, but in order to judge the quality of the software, not only the bug found in the test but also the bug not found in the test = information on the bug still latent in the software It’s very important.

Let’s think a little about why the information on potential bugs is important. When judging the quality of software from the viewpoint of bugs, the less bugs that remain in the software, the better the quality . 　There are two types of bugs that remain in the software: (1 ) unfixed bugs that have already been found but have not been fixed in time, and (2) bugs that have not been found yet but are latent in the software . The number and contents of (1) are known, but the number and contents of (2) are unknown because they have not been found. Since it is unknown, there may be zero potential bugs or 100 potential bugs. In other words, if you do not know the status of potential bugs, you will not know whether the quality of the software is good or bad.

The quality of the software depends on how many potential bugs there are

In order to check whether the quality of the software has improved to a level where it is okay to release it, it is actually necessary to check whether this potential bug is sufficiently small . For that reason, have you thoroughly tested the quantity and quality to identify bugs? Or, is the detection status of this bug comparable to similar software development so far? Or, based on the content of this test and its results, I will try to qualitatively estimate that there are almost no potential bugs left .

And one of the means to quantitatively estimate that there are no latent bugs is to estimate the number of latent bugs using the Software Reliability Growth Model (SRGM) . By using the reliability growth curve, you can calculate the number of latent bugs and the estimated percentage of all bugs found in the tests so far, so you can quantitatively “estimate" the status of latent bugs. You can do it.

The reliability growth curve is one of the bug curves and estimates the number of bugs in the future.

The reliability growth curve is a curve that assumes an S-shaped curve with the amount of tests (number of test items and test man-hours) on the horizontal axis and the cumulative number of bugs detected on the vertical axis. (In the initial stage of the test, it does not become an S-shaped curve and rises vigorously …) It is sometimes called a bug curve in the sense of a graph that visualizes the detection status of bugs , and it is also called an S-shaped curve . Gombelts curve and logistic curve that draw a curve are also sometimes used for bug curves.

Whether it is a reliability growth curve or a Gombelz curve, the basic idea of ​​estimating latent bugs using a bug curve is as follows: ( 1 ) Plot the test results (= test amount and cumulative number of detected bugs) so far on a graph, and (2) It is said that the curve of the curve is applied so that it follows the actual value, and (3) if the test is continued as it is , the bug will be detected by the number of cases along the curve .

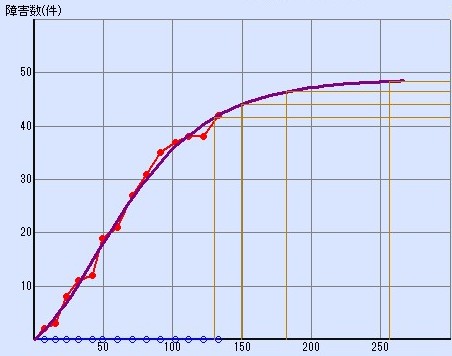
An example of the reliability growth curve is the graph below. The line graph part plotted in red is (1) the test results, the horizontal axis is 130 and the vertical axis is 42. The reliability growth curve applied to the plot of this achievement is the purple curve. And the horizontal axis of this curve is 130 and the part on the right side is ③ Estimate of the number of bugs found in future tests. This estimate suggests that if you continue testing, you’ll find up to 48 bugs. Since we have found 42 bugs so far, it means that we will find 6 more bugs.

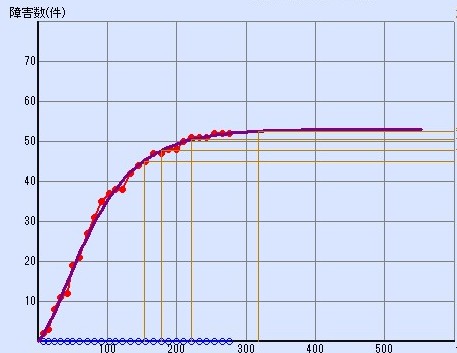
In the above example, the curve is not over because it is based on the actual results of the state where the test has not progressed sufficiently. It is estimated that there are still potential bugs, so testing should continue. If you draw a reliability growth curve based on the test data when you continue the test from this state and increase the actual number of bug detection, the graph will be as follows. The extension of the purple curve that extends beyond the performance red plot is estimated to lie almost horizontally and no more bugs can be found.

If you write a reliability growth curve, you can quantify the number of potential bugs and what percentage of bugs are currently detected.

Reliability Growth curves to write a, of the curve asymptotes from the value of the Y-axis value of (near-Nuisance line as possible to the curve), the total bug count ( of = all bugs number detected in the test) estimate is understandable increase. Subtracting the number of currently detected bugs from the total number of bugs value gives you the number of potential bugs that may be detected in future tests . Also, if you calculate (the number of bugs detected so far x 100) / the total number of bugs , the current bug detection rate (= what percentage of the total number of bugs detected so far) is calculated. I can do it.

Father Gutara creates a reliability growth curve by inputting the test results (man-hours and number of bugs detected), and then calculates the total number of bugs and the current bug detection rate, a software tool called SRGM2. uses , Created a graph and calculated the total number of bugs and bug detection rate. This soft tool covers exponential model, super exponential model, delayed S-shaped model, Gompelz curve, logistic curve, familiar S-shaped model, selects the optimum curve model based on the input actual value, and selects the optimum curve model. It was very easy to use because it determines the parameters of the graph and creates the graph.

Experience shows that if the bug detection rate does not exceed 95% to 98%, there are still potential bugs and there is a high risk that the bugs will cause problems in the market, so it is better to stop releasing the software. I used it as a guideline for release judgment because it felt good (continue testing and get rid of bugs).

Is the Confidence Growth Curve Estimate Reliable?

Using the confidence growth curve to estimate the total number of bugs, the number of potential bugs, and the bug detection rate, we are only estimating the number of bugs that will be detected in future tests that have not yet occurred . There is no theoretical proof that the number of bugs detected in the future will follow the reliability growth curve, so in short, it is a world of eight hits and eight hits.

Still, as I wrote in another article, it has the advantage of being able to quantify the number of potential bugs that are very important for software quality , making it easy to use to judge whether quality is good or bad, and many developments. Based on the empirical rule that the correlation with the quality of the software is good as it is when actually using it in the project and accumulating the usage record , Father Gutara thinks that the reliability growth curve is useful as it is, and decides the release. I used it for.